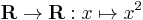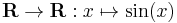Bijection, injection and surjection
In mathematics, injections, surjections and bijections are classes of functions distinguished by the manner in which arguments (input expressions from the domain) and images (output expressions from the codomain) are related or mapped to each other.
A function maps elements from its domain to elements in its codomain.
- A function
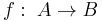 is injective (one-to-one) if every element of the codomain is mapped to by at most one element of the domain. Notationally,
is injective (one-to-one) if every element of the codomain is mapped to by at most one element of the domain. Notationally,
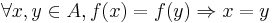 or, equivalently,
or, equivalently,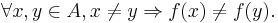
An injective function is an injection.
- A function is surjective (onto) if every element of the codomain is mapped to by at least one element of the domain. (That is, the image and the codomain of the function are equal.) Notationally,
A surjective function is a surjection.
- A function is bijective (one-to-one and onto or one-to-one correspondence) if every element of the codomain is mapped to by exactly one element of the domain. (That is, the function is both injective and surjective.) A bijective function is a bijection.
An injective function need not be surjective (not all elements of the codomain may be associated with arguments), and a surjective function need not be injective (some images may be associated with more than one argument). The four possible combinations of injective and surjective features are illustrated in the following diagrams.
Contents |
Injection
A function is injective (one-to-one) if every possible element of the codomain is mapped to by at most one argument. Equivalently, a function is injective if it maps distinct arguments to distinct images. An injective function is an injection. The formal definition is the following.
- The function
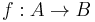 is injective iff for all
is injective iff for all 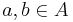 , we have
, we have 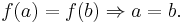
- A function f : A → B is injective if and only if A is empty or f is left-invertible; that is, there is a function g : f(A) → A such that g o f = identity function on A. Here f(A) is the image of f.
- Since every function is surjective when its codomain is restricted to its image, every injection induces a bijection onto its image. More precisely, every injection f : A → B can be factored as a bijection followed by an inclusion as follows. Let fR : A → f(A) be f with codomain restricted to its image, and let i : f(A) → B be the inclusion map from f(A) into B. Then f = i o fR. A dual factorisation is given for surjections below.
- The composition of two injections is again an injection, but if g o f is injective, then it can only be concluded that f is injective. See the figure at right.
- Every embedding is injective.
Surjection
A function is surjective (onto) if every possible image is mapped to by at least one argument. In other words, every element in the codomain has non-empty preimage. Equivalently, a function is surjective if its image is equal to its codomain. A surjective function is a surjection. The formal definition is the following.
- The function
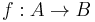 is surjective iff for all
is surjective iff for all 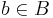 , there is
, there is 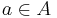 such that
such that 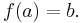
- A function f : A → B is surjective if and only if it is right-invertible, that is, if and only if there is a function g: B → A such that f o g = identity function on B. (This statement is equivalent to the axiom of choice.)
- By collapsing all arguments mapping to a given fixed image, every surjection induces a bijection defined on a quotient of its domain. More precisely, every surjection f : A → B can be factored as a projection followed by a bijection as follows. Let A/~ be the equivalence classes of A under the following equivalence relation: x ~ y if and only if f(x) = f(y). Equivalently, A/~ is the set of all preimages under f. Let P(~) : A → A/~ be the projection map which sends each x in A to its equivalence class [x]~, and let fP : A/~ → B be the well-defined function given by fP([x]~) = f(x). Then f = fP o P(~). A dual factorisation is given for injections above.
- The composition of two surjections is again a surjection, but if g o f is surjective, then it can only be concluded that g is surjective. See the figure at right*.
Bijection
A function is bijective if it is both injective and surjective. A bijective function is a bijection (one-to-one correspondence). A function is bijective if and only if every possible image is mapped to by exactly one argument. This equivalent condition is formally expressed as follows.
- The function
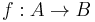 is bijective iff for all
is bijective iff for all 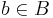 , there is a unique
, there is a unique 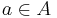 such that
such that 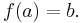
- A function f : A → B is bijective if and only if it is invertible, that is, there is a function g: B → A such that g o f = identity function on A and f o g = identity function on B. This function maps each image to its unique preimage.
- The composition of two bijections is again a bijection, but if g o f is a bijection, then it can only be concluded that f is injective and g is surjective. (See the figure at right and the remarks above regarding injections and surjections.)
- The bijections from a set to itself form a group under composition, called the symmetric group.
Cardinality
Suppose you want to define what it means for two sets to "have the same number of elements". One way to do this is to say that two sets "have the same number of elements" if and only if all the elements of one set can be paired with the elements of the other, in such a way that each element is paired with exactly one element. Accordingly, we can define two sets to "have the same number of elements" if there is a bijection between them. We say that the two sets have the same cardinality.
Likewise, we can say that set  "has fewer than or the same number of elements" as set
"has fewer than or the same number of elements" as set  if there is an injection from
if there is an injection from  to
to  . We can also say that set
. We can also say that set  "has fewer than the number of elements" in set
"has fewer than the number of elements" in set  if there is an injection from
if there is an injection from  to
to  but not a bijection between
but not a bijection between  and
and  .
.
Examples
It is important to specify the domain and codomain of each function since by changing these, functions which we think of as the same may have different jectivity.
Injective and surjective (bijective)
- For every set A the identity function idA and thus specifically
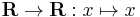 .
. 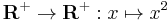 and thus also its inverse
and thus also its inverse 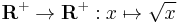 .
.- The exponential function
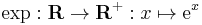 and thus also its inverse the natural logarithm
and thus also its inverse the natural logarithm 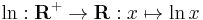
Injective and non-surjective
- The exponential function
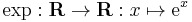
Non-injective and surjective
Non-injective and non-surjective
Properties
- For every function f, subset A of the domain and subset B of the codomain we have A ⊂ f −1(f(A)) and f(f −1(B)) ⊂ B. If f is injective we have A = f −1(f(A)) and if f is surjective we have f(f −1(B)) = B.
- For every function h : A → C we can define a surjection H : A → h(A) : a → h(a) and an injection I : h(A) → C : a → a. It follows that h = I ∘ H. This decomposition is unique up to isomorphism.
Category theory
In the category of sets, injections, surjections, and bijections correspond precisely to monomorphisms, epimorphisms, and isomorphisms, respectively.
History
This terminology was originally coined by the Bourbaki group.
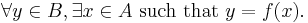
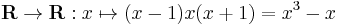
![\mathbf{R} \to [-1,1]�: x \mapsto \sin(x)](/2012-wikipedia_en_all_nopic_01_2012/I/7fed756a0099c8fb36213eccc17ad0c6.png)